How I ensure every Daily Q-less puzzle is solvable

This is a technical overview related to Daily Q-less, my web adaptation of the Q-less word puzzle game.

The most frustrating part of the Q-less dice game is that, some small percentage of the time, the letters you roll have no valid solution.¹ If this happened in Daily Q-less, the Snyder family group chat would never let me hear the end of it. But I don’t want to pre-solve every day’s roll myself to verify it. That’s what programming is for.

Why this is hard

When I solve a Q-less roll, here’s how I go about it:

1. Find a word (hopefully using some of the more difficult letters, like V or X).
2. Find a good word that intersects it.
3. Find a third word that intersects one of the first two words.
4. See if my remaining letters (if any) can fit anywhere.
5. If they don’t fit, go back to an earlier step and try a different word.

So why can’t a computer program do the same thing? Well, it can—if you’re willing to wait a few hours. This was my first approach, but it never finished running, because there are so many arrangements of words that never actually lead to a solution. Some approximate math:

• A typical roll has about 100 legal words it can form.
• After placing the first word, we typically have 3-5 intersection points, and we have to check which of the 100 legal words use exactly one of the letters already used. This step mostly can’t be memoized.
• Now that we’ve placed a second word, we typically have 5-8 intersection points. Some placements of the next word could produce a grid with a 2-letter fragment, which is isn’t allowed, but we can’t actually exclude those placements. Why? Because later words can turn those 2-letter fragments into 3-letter words. Take the solution on the right in the below image. It’s impossible to construct that solution without the grid having a 2-letter fragment at some point.

• Once we have three words in the grid, it becomes even more complicated to see where the remaining letters can fit, because a newly placed word might intersect two other words at once. And we also need to start checking that the spaces before and after the word are empty.
• Odds are, at some point during this process, we get stuck with some letters we can’t use. Even if we do use all the letters, we need to ensure every 2-letter fragment became part of a valid 3-letter word. If either of these checks fail, we have to backtrack and try a different word.

I don’t know the typical number of branches—it takes my laptop too long to count them all—but I would estimate something on the order of millions, depending on the roll, with thousands of legality checks needed for each branch. So, unless you have a supercomputer or a lot of patience, the problem requires a different approach.

What did work

The better solution was to split the solver into two stages. The first stage ignores the letters and computes just the legal grid shapes a solution can take. This is a much more tractable problem than the above, because it reduces the branching factor and reduces the overhead per branch.

Here’s the new algorithm:

1. Put down a letter at the origin $(0, 0)$.
2. Find all the places we can put a letter adjacent to an existing letter.²
3. Check whether any of these grids are functionally identical.³ If so, get rid of the duplicates.
4. Repeat until all 12 letters are added.
5. Finally, remove any grids with a 2-letter fragment remaining.

There are only a couple thousand branches by the end, so despite the overhead from duplicate checking, it only takes a few minutes. And the best part is: it only has to be done once! I stored all 6,223 distinct grids as a JSON file, noting each word’s length, location, intersection points, and whether it’s across or down.

Then, using that set of grid shapes, here’s how to solve a Q-less roll:

1. List of all possible words using those letters.⁴
2. Select a grid.
3. Slot a word into the first word slot in the grid.
4. Slot a word into the next slot using the remaining letters and respecting all intersecting letters that need to match.
5. Repeat until all letters are used, or backtrack if there are no legal words to put in the next slot.
6. If the chosen grid doesn’t work, try another.

This works, and it only takes a matter of seconds to find all solutions. To improve performance, I ordered the grids by a rough measure of $(\textrm{likelihood of solution}) / (\textrm{average number of branches})$. While the grid that is most likely to have a solution looks like this:

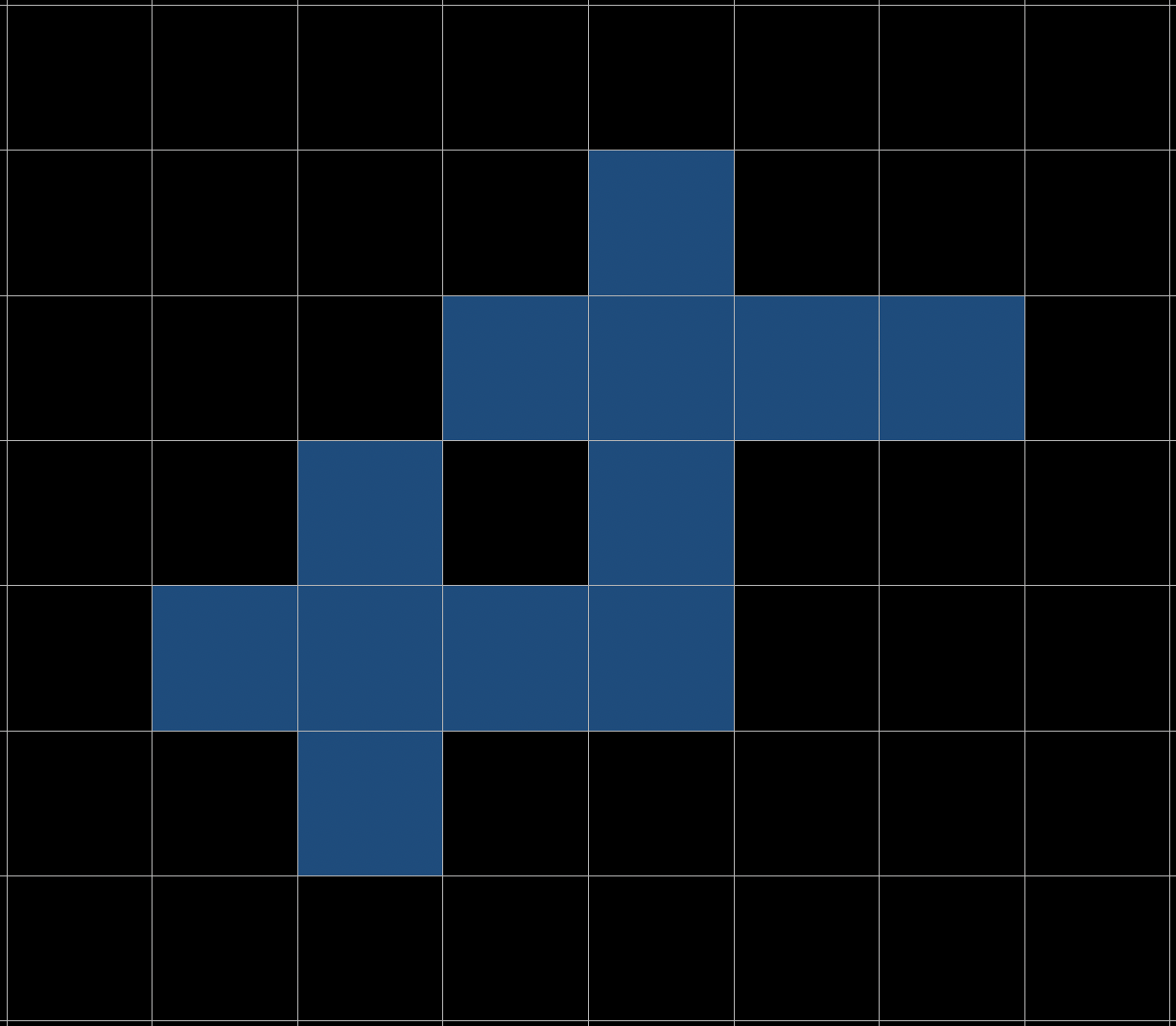
It tends to have a large number of branches, whereas the most efficient grid looks like this:

It doesn’t have solutions as often, but because it only has 3 word slots, it’s much quicker.

Other benefits of the solver

The solver also allows me to roughly quantify a roll’s difficulty. Some rolls have thousands of solutions, and some have only one (or none). To approximate how difficult a roll is, the solver counts the number of grids it needs to check before finding ten distinct solutions. Rolls are assigned to days of the week based on that count:

• <10 grids: discard, too easy
• 10–20 grids: Monday
• 21–150 grids: Tuesday
• 151–600 grids: Wednesday
• 300+ grids: Thursday⁵
• 600+ grids: Friday
• <10 solutions found: Saturday
• <10 solutions found: Sunday⁵

So, much like the New York Times crossword, the Daily Q-less scales in difficulty throughout the week. If I show the game to a friend, I make sure their first try is on a Monday or Tuesday so they can ease into it. Meanwhile, I like to solve it from Thursday through Sunday when it’s hardest.

Wow! What an article. If this got you interested in Daily Q-less, I encourage you to try it out! And if you think it demonstrates my excellent coding and problem-solving ability, I encourage you to hire me. The code for Daily Q-less and my other games is open-source, and you can view it on GitHub. The file discussed in this blog post is here.